레이저 빔 익스팬더
본 내용은 레이저 옵틱스 리소스 가이드의 기타 단원에 해당합니다.
레이저 빔 익스팬더는 시준된 입력빔을 직경이 더 큰 시준 출력빔으로 확장시켜줍니다. 빔 익스팬더는 주로 레이저 스캐닝, 간섭계, 원격 감지 등과 같은 용도에 사용됩니다. 현대식 레이저 빔 익스팬더는 제대로 정립된 광학 망원경의 개념을 바탕으로 개발된 afocal system입니다. 이러한 시스템에서 피사체의 광선은 내부 옵틱의 광축과 평행하게 입사하고 평행하게 출사합니다. 이는 시스템 전체가 초점 거리를 가지고 있지 않음을 의미합니다.
이론: 망원경
광학 망원경은 일반적으로 우주 공간에 있는 천체와 같이 원거리 피사체를 관찰할 때 사용되며 유형에 따라 굴절 망원경과 반사 망원경 두 가지로 나뉩니다. 굴절 망원경은 렌즈를 사용해 빛을 굴절 및 굴곡시키는 데 반해 반사 망원경은 미러를 사용해 빛을 반사시킵니다.
굴절 망원경은 범주에 따라 케플러식 망원경과 갈릴레이식 망원경 두 가지로 구분됩니다. 케플러식 망원경(Keplerian telescope)은 초점 거리의 합으로 분리된 양수 초점 거리 렌즈로 구성됩니다(그림 1). 관찰하고자 하는 피사체나 소스 이미지에 가장 가까운 렌즈를 대물렌즈라고 하며 관찰자의 눈 또는 생성된 이미지에 가장 가까운 렌즈를 이미지 렌즈라고 합니다.
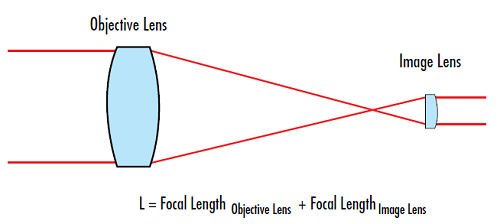
그림 1: 케플러식 디자인
갈릴레이식 망원경(Galilean telescope)은 초점 거리의 합으로 분리되어 있는 positive lens와 negative lens로 구성됩니다(그림 2). 하지만 이 두 렌즈 중 하나는 음의 렌즈이기 때문에 렌즈간 간격이 케플러식 망원경에서의 간격보다 훨씬 더 짧습니다. 두 렌즈의 유효 초점 거리를 사용해 전체 길이의 근사치를 구할 수도 있지만 후초점 거리를 사용해야만 가장 정확한 길이를 알아낼 수 있습니다.
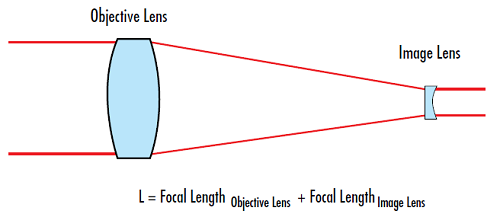
그림 2: 갈릴레이식 디자인
망원경의 배율 또는 배율의 역치는 대물 렌즈와 이미지 렌즈의 초점 거리를 기초로 합니다.
배율이 1보다 클 경우에 망원경은 이미지를 확대시킵니다. 배율이 1보다 작을 경우에 망원경은 이미지를 축소시킵니다.
이론: LASER BEAM EXPANDER
레이저 빔 익스팬더에서 대물 렌즈와 이미지 렌즈는 서로 반대로 위치합니다. 케플러식 빔 익스팬더는 시준된 입력빔이 대물 렌즈와 이미지 렌즈 사이에 있는 한 지점에 초점을 맞추도록 설계되어 레이저의 에너지를 집중시켜야 하는 시스템 내에서 점(point)을 생성합니다(그림 3). 초점이 집중된 스폿은 렌즈 사이에 있는 공기를 가열해 광선이 광경로를 벗어나도록 하며 이는 잠재적으로 웨이브프론트 에러를 야기할 수 있습니다. 레이저 파워가 매우 높은 고출력 어플리케이션에서는 초점을 맺는 지점에서 공기의 이온화 또한 문제가 될 수 있습니다. 이와 같은 이유로 대다수의 빔 익스팬더는 갈릴레이식 디자인을 적용하거나 혹은 변형된 갈릴레이식 디자인을 적용합니다(그림 4). 하지만 케플러식 디자인은 공간 필터(spatial filter)를 간단하게 배치할 수 있도록 초점(focus point)을 제공하기 때문에 공간 필터링이 필요한 레이저 용도에는 여전히 케플러식 디자인이 유용합니다.
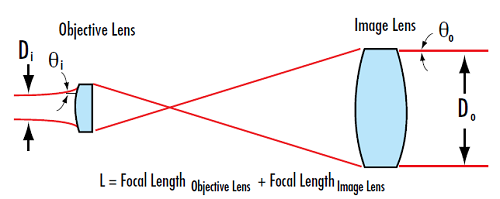
그림 3: 케플러식 빔 익스팬더는 내부 초점을 가지고 있어 고출력 용도에 유해하지만 저출력 용도의 공간 필터링에는 유용함
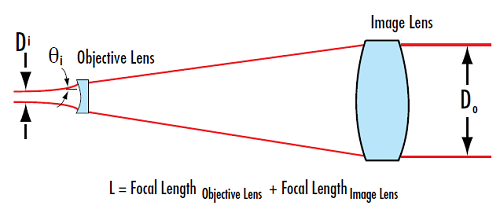
그림 4: 갈릴레이식 빔 익스팬더에는 내부 초점이 없어 고출력 레이저 용도에 적합
레이저 빔 익스팬더 용도에서 케플러식 또는 갈릴레이식 디자인을 사용할 때는 출력빔의 발산을 계산해내는 것이 중요합니다. 이는 산출된 발산을 이용해 완벽하게 시준된 광원과의 편차를 구할 수 있기 때문입니다. 빔의 발산은 입력빔과 출력빔의 직경에 따라 달라집니다.
배율(MP)은 빔의 발산 또는 빔의 직경을 바탕으로 기술할 수 있습니다.
방정식 4와 방정식 5를 해석할 시 출력빔의 직경(D0)이 증가하면 출력빔의 발산(θ0)은 감소하고 이와 반대일 경우에도 마찬가지임을 알 수 있습니다. 따라서 빔 익스팬더를 사용해 빔을 최소화하면 빔의 직경은 감소하지만 레이저의 발산은 증가하게 됩니다. 이는 작은 빔을 사용하는 대가로 큰 발산각을 얻게 되는 것이라고 볼 수 있습니다.
이외에도 특정 작동 거리(L)에서 출력빔의 직경을 산출할 수 있어야 합니다. 출력빔의 직경은 특정 작동 거리(L)만큼 떨어진 곳에서 입력빔의 직경 및 빔의 발산과 상관관계에 있습니다(그림 5).
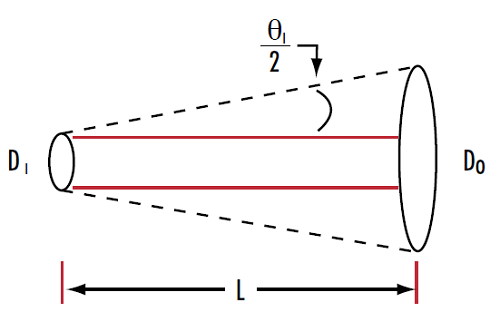
그림 5: 레이저의 입력빔 직경과 발산을 사용하면 특정 작동 거리에서 출력빔의 직경 산출 가능
레이저 빔의 발산은 반각(half angle)으로 표시되며 이 때문에 방정식 6의 두 번째 항에는 인수 2가 필요합니다.
빔 익스팬더는 배율에 따라 입력빔을 증가시키고 입력 발산을 감소시킵니다. 방정식 4와 5를 방정식 6으로 대체하면 다음과 같은 결과를 얻을 수 있습니다.
어플리케이션 1: 출력 밀도 감소
빔 익스팬더는 빔 내에 있는 총 에너지에 큰 영향을 미치지 않으면서 배율에 따라 빔의 영역을 2차로 증가시킵니다. 그 결과 빔의 출력 밀도와 방사조도가 감소하여 레이저 부품의 수명이 증가하고 레이저 유도 손상 가능성이 낮아져 광학 코팅과 옵틱을 좀 더 경제적으로 사용할 수 있게 됩니다.
어플리케이션 2: 빔의 최소화 원거리에서의 직경
직관적으로 보이지 않을 수도 있지만 빔 익스팬더를 사용해 레이저의 직경을 증가시키면 레이저 구경에서 멀리 떨어진 곳에 위치한 빔의 직경이 작아질 수 있습니다. 빔 익스팬더는 명확히 지정된 확장 파워로 입력 레이저 빔을 증가시키고 또한 동일한 확장 파워로 발산 또한 감소시키기 때문에 결과적으로 원거리에서 시준빔을 더 작게 만듭니다.
예시
앞서 언급한 빔 익스팬더 관련 방정식을 확인하기 위해 숫자를 대입해 설명한 예:
초기 매개변수
빔 익스팬더의 배율 = MP = 10X
입력빔의 직경 = 1mm
입력빔의 발산 = 0.5mrad
작동 거리 = L = 100m
산출된 매개변수
출력빔의 직경
방정식 6을 이용하면 빔 익스팬더를 사용하지 않고도 이 값을 빔의 직경과 비교할 수 있습니다.
10X 빔 익스팬더를 사용하면 100m 떨어진 곳에 있는 출력빔의 직경을 빔 익스팬더를 사용하지 않는 동일한 레이저보다 5배까지 줄일 수 있음을 알 수 있습니다.
어플리케이션 3: 초점을 맺는 스폿 크기 최소화
스폿의 크기는 일반적으로 최대 방사조도의 중심점에서부터 강도가 초기 값의 1/e2까지 떨어지는 지점까지의 반경 거리로 정의됩니다 (그림 6). 이상적인 렌즈가 초점을 맺는 스폿의 크기는 파장(λ), 렌즈의 초점 거리(f), 입력빔의 직경(DI), 렌즈의 굴절률(n)을 비롯해 이상적인 가우시안 빔의 변화 정도를 나타내는 빔의 M2 계수를 이용해 계산할 수 있습니다.
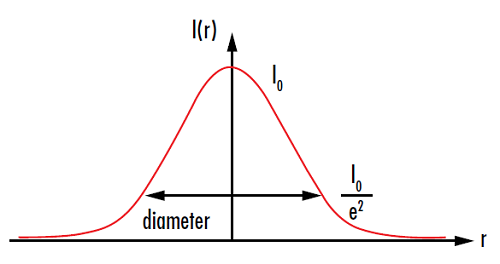
그림 6: 스폿의 크기는 일반적으로 강도 I(r)가 초기 값 I0의 1/e2까지 떨어지는 지점에서 측정됨
스폿의 크기는 그림 7에 나와 있듯이 각각 적색과 청색으로 표시된 회절과 광학 수차를 조합해서 기본적으로 결정됩니다. 일반적으로 레이저 빔을 포커싱할 때 우세하게 나타나는 유일한 수차 유형을 구면 수차라고 가정하기 때문에 방정식 11에서는 구면 수차만을 참작합니다. 회절과 관련해서는 초점 거리가 짧을수록 스폿의 크기가 작아집니다. 이때 더 중요한 것은 입력빔의 직경이 커질수록 스폿 크기 또한 작아진다는 점입니다.
시스템 내에서 빔을 확장시키면 입력빔(D)은 인수 m에 의해 증가하고 발산은 인수 m에 의해 감소합니다. 이러한 빔을 작은 점으로까지 포커싱하면 이때 스폿은 회절이 제한된 이상적인 스폿에 적합한 비확장 빔의 인수보다 작은 인수 m이 됩니다. 다만 스폿은 입력빔의 직경에 따라 증가하기 때문에 대신 구면 수차로 절충이 됩니다.
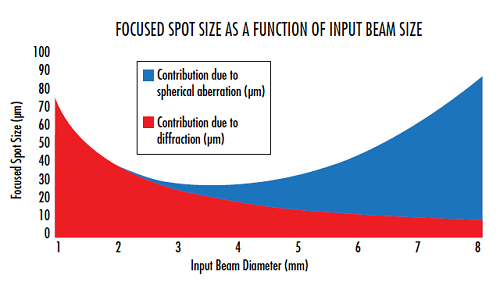
그림 7: 크기가 작은 입력빔의 직경에서 초점이 맺히는 스폿의 크기는 회절 한계를 나타냄. 입력빔의 직경이 증가하면서 구면 수차는 스폿의 크기를 제어하기 시작함
어플리케이션 4: 레이저 빔의 크기 보정
가변형 레이저 빔 익스팬더는 대개 용도에 따라서 레이저 빔의 크기를 표준화하는 데 사용됩니다. 레이저는 명확히 지정된 빔의 직경을 생성할 뿐만 아니라 이러한 직경에 맞는 허용오차 또한 가지고 있습니다. 다양한 시스템에서 설정된 빔의 직경을 광경로 보다 훨씬 더 아래에서 달성하기 위해서는 가변형 빔 익스팬더를 사용해야 빔의 크기에 따른 레이저간의 가변성을 보정할 수 있습니다.
빔 익스팬더의 선택 기준
용도에 맞는 빔 익스팬더를 선택할 때에는 정확한 성능을 발휘할 수 있도록 특정한 기준이 마련되어야 합니다.
슬라이드식 vs. 회전식 포커스 메커니즘:
빔 익스팬더의 초점을 맞추거나 가변형 빔 익스팬더의 배율을 변경할 때 사용되는 메커니즘은 유형에 따라 일반적으로 sliding과 rotating으로 분류됩니다. Threaded focusing tube와 같은 회전식 포커스 메커니즘은 수평으로 움직이는 동안 광학 요소를 회전시킵니다. 이와 같은 메커니즘은 단순화된 기계적 구조로 슬라이드식 포커스 메커니즘보다 비용이 적게 들지만 광학 요소의 회전으로 인해 잠재적 빔의 이탈을 야기할 수 있습니다(그림 8).
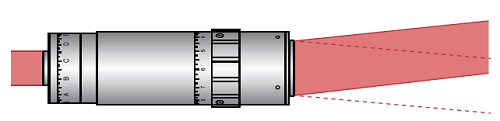
그림 8: 회전식 초점 메커니즘으로 인해 야기된 빔의 이탈을 과장되게 표현한 그림
Helicoid barrel과 같은 슬라이드식 포커스 메커니즘은 회전 이동 없이도 내부 옵틱을 움직일 수 있어 빔의 이탈을 최소화합니다. 하지만 이 메커니즘은 회전식 포커스 메커니즘보다 기계적 구조가 더 복잡하기 때문에 시스템의 비용을 증가시킵니다. 또한 제대로 설계되지 않은 슬라이드형 옵틱의 경우에는 기계 내에서 지나치게 자유로운 움직임을 갖게 될 수도 있습니다. 이처럼 미흡한 디자인에서 발생하는 포인팅 에러는 조정 시 회전을 하지는 않지만 회전형 옵틱 또는 올바르게 설계된 슬라이드형 옵틱의 에러보다 더 크게 부각될 것입니다.
내부 초점:
케플러식 빔 익스팬더는 고출력 시스템에 문제가 될 수 있는 내부 초점을 가지고 있습니다. 초점이 집중적으로 맺히는 스폿은 공기를 이온화하거나 혹은 광선의 경로 이탈을 유도하는 열로 인해 발생하는 웨이브프론트 에러를 야기할 수 있습니다. 이 때문에 대다수의 빔 익스팬더는 내부 포커싱으로부터 발생하는 복잡한 문제를 피하기 위해 갈릴레이식 디자인을 채택합니다. 하지만 케플러식 빔 익스팬더가 가지고 있는 내부 초점 능력 때문에 특정 어플리케이션에서는 케플러식 디자인에만 적용할 수 있는 공간 필터링이 필요하기도 합니다.
반사형 vs. 투과형:
반사형 빔 익스팬더는 투과형 렌즈 대신에 곡면 미러를 사용해 빔을 확장시킵니다(그림 9). 반사형 빔 익스팬더는 투과형 빔 익스팬더보다 사용도가 낮지만 특정 용도에 유용한 몇 가지 이점을 가지고 있습니다. 반사형 빔 익스팬더는 색 수차가 발생하지 않는 데 반해 투과형 빔 익스팬더는 배율 및 출력빔의 시준이 파장에 따라 달라집니다. 레이저는 단일 파장에서 광선을 발사하는 경향이 있기 때문에 다수의 레이저 용도에는 투과형 빔 익스팬터가 적합하지 않지만 광대역 용도에는 매우 중요할 수 있습니다. 반사형 빔 익스팬더의 무채색 성능은 다중 레이저 시스템과 일부 가변 파장 레이저 그리고 초고속 레이저에 반드시 필요한 요건입니다. 초고속 레이저는 펄스 지속 시간이 매우 짧기 때문에 본질적으로 다른 레이저보다 더 넓은 파장 범위를 가지고 있습니다. Quantum cascade laser는 투과 옵션이 작동 파장에 존재하지 않을 수도 있어 반사형 빔 익스팬더를 사용하는 것이 보다 유리합니다.
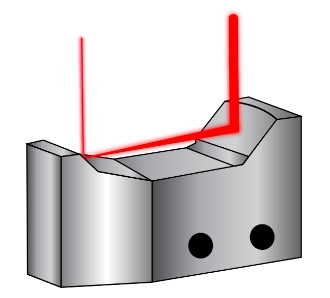
그림 9: 투과형 빔 익스팬더와 달리 Canopus Reflective Beam Expander의 곡면 미러는 입사하는 레이저 빔을 확장시킴. 빔 익스팬더 측면에 있는 홀은 통합 장착 기능을 제공함
빔 익스팬더 선택 가이드
에드몬드 옵틱스 제품
TECHSPEC® Scorpii Nd:YAG Beam Expanders는 비용을 중요시하는 용도를 위해 고안된 제품입니다.. YAG 파장에서 회절 한계 성능을 갖는 2-element Galilean design이 특징인 이 Scorpii Nd:YAG Beam Expanders는 2X - 10X의 다양한 배율을 제공함에 따라 프로토타이핑 및 OEM 통합 용도에 이상적으로 사용할 수 있습니다.
TECHSPEC® Vega Laser Line Beam Expanders는 최대 4 mm의 aperture에 대해 설계 파장에서 λ/10의 성능을 발휘하는 우수한 가치를 제공합니다. 최저 266 nm의 Nd:YAG harmonics에 대한 레이저 라인 V-코팅을 특징으로 하는 이 갈릴레이 디자인(Galilean Design)은 용융 실리카 소재의 엘레먼트를 사용함에 따라 발산각 조절이 가능합니다.
갈릴레이 망원경 디자인을 레이저 빔 익스팬더에 적용한 예를 몇몇 에드몬드 옵틱스 제품에서 찾아볼 수 있으며 이 제품들은 레이저 빔을 시준하고 초점을 맞추는 데 사용됩니다. 당사의 TECHSPEC® Arcturus HeNe Beam Expanders는 negative lens와 achromatic lens로 구성된 단순한 two-lens 디자인입니다. 내부 광학 요소의 도면이 참고로 표시되어 있습니다.
TECHSPEC® Vega Broadband Beam Expanders는 tunable laser 광원에 이상적인 광대역 발산각 조절 디자인을 특징으로 합니다. 이 빔 빔스팬더는 광범위한 파장에 최적화되고 λ/10의 투과 웨이브프론트 에러를 제공하며 내부 초점 조절 시 고스트 이미지가 발생하지 않아 고출력 레이저 광원과 호환이 가능합니다.
TECHSPEC® Draconis Broadband Beam Expanders는 긴 작동 거리에서 시준되거나 초점을 맺는 레이저 빔 직경의 생성 능력을 강화시키는 전매특허 다중 요소 렌즈 디자인을 이용해 단순한 two-lens 디자인을 개선시켜줍니다.
특허 출원 중인 TECHSPEC® Canopus Reflective Beam Expanders는 통합 정렬 기능을 다양하게 갖추고 있어 마운트가 용이합니다. 이 빔 익스팬더는 자외선부터 적외선에 이르는 구간(250nm - 10μm)에서 웨이브프론트 왜곡을 최소화하면서 광대역 성능을 제공합니다. 모놀리식 구조로 설계되어 온도의 변화와 무관하게 성능 안정성이 뛰어납니다.
참고 자료
- Greivenkamp, John E. Field Guide to Geometrical Optics. Vol. FG01. Bellingham, WA: SPIE—The International Society for Optical Engineers, 2004.
- Smith, Warren J. Modern Optical Engineering. 3rd ed. New York, NY: McGraw-Hill Education, 2000.













 이전 단원
이전 단원 


















본사 및 지사별 연락처 확인하기
견적 요청 도구
재고 번호 입력 필요
Copyright 2023, 에드몬드옵틱스코리아 사업자 등록번호: 110-81-74657 | 대표이사: 앙텍하우 | 통신판매업 신고번호: 제 2022-서울마포-0965호, 서울특별시 마포구 월드컵북로 21, 7층 (서교동, 풍성빌딩)