극초단 레이저 – 극초단 결맞음(Ultrafast Coherence)의 기본 원리
원자(atom)의 개념은 24세기 전인 고대 그리스 철학자 레우키포스(Leucippus)와 데모크리토스(Democritus)에 의해 정립되었습니다.1 그러나 원자의 움직임을 관찰하고 조작하는 것은 20세기 후반이 되어서야 가능해졌습니다.2 1Å의 거리에서 대략 10 km/s의 기본 속도로 원자 규모의 역학을 다루는 데 필요한 시간 분해능은 10 펨토초(10×10-15초)입니다. 이에 따라 원자와 분자를 시각화하고 이를 다루기 위해서는 지속 시간이 대략 핵 운동 정도 되는 레이저 펄스가 필요합니다. 레이저 기술이 급속도로 발전하면서 현재는 수 펨토초에서 수십 아토초(10×10-18초) 사이의 펄스를 생산할 수 있게 되었습니다. 이러한 극초단 펄스로 인해 원자와 전자에 관한 직접 연구 및 정밀 조작이 가능해지면서 기존에는 접근조차 할 수 없었던 영역까지 과학과 기술의 한계를 허물 수 있게 되었습니다.
레이저는 이득매질(gain medium)을 사용하는 광증폭(예: Ti:sapphire crystal)과 공진기(cavitiy)로 보장되는 피드백(예: 미러 2개)의 두 가지 일반 원리로 작동합니다. 여기된 이득매질에서 빛이 증폭됨에 따라 공진기의 피드백으로 인해 부분적으로 투과하는 강렬한 레이저 빔이 생성됩니다(그림 1).
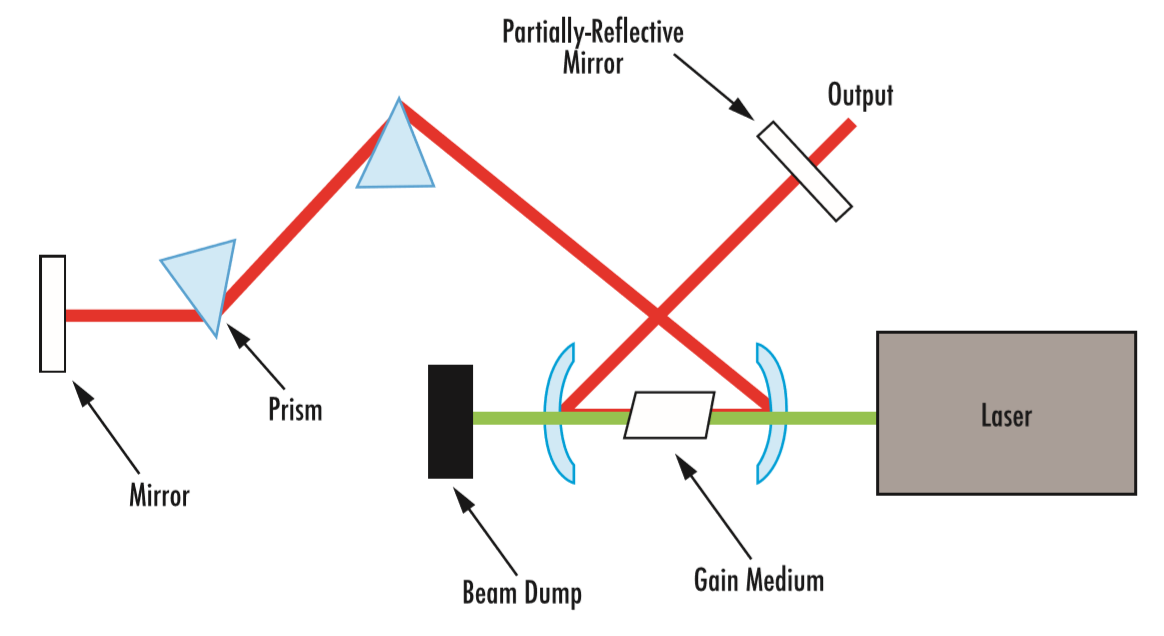
그림 1: 연속파(CW), 제2고조파 발생(SHG: second-harmonic generation), Nd:YAG 레이저를 사용하는 ultrafast laser oscillator의 일반적인 광학 세팅 방식
극초단 펄스(ultrashort pulse)는 모드 수가 많은 광파 또는 광파장(λ) 절반의 정수배가 모드 동기(mode-locking)로도 알려진 동상 중첩(in-phase superposition)을 통해 간섭성을 띠며 방출될 때 생성됩니다. 극초단 펄스의 넓은 에너지 대역폭은 시간 에너지의 정밀도가 푸리에 변환(Fourier transform)에 의해 제한되는 광자 고유의 파동 특성으로부터 발생한다는 불확실성 원리에서 비롯됩니다. 극초단 펄스의 에너지(E=hc/λ)는 대역폭 내에서 여러 옥타브에 걸쳐있을 수 있기 때문에 이때 중요하게 짚고 넘어가야 할 것은 넓은 펄스가 간섭성을 유지하는지 여부입니다. 간섭의 개념은 광파와 원자/전자 집단 사이에서 간섭 효과를 보장하기 위해 극초단 규모에서의 광물질(light-matter) 상호작용이 상당히 중요합니다. 이러한 간섭은 파동들 사이의 위상차에 따라 보강 간섭과 상쇄 간섭으로 나뉠 수 있습니다. 3
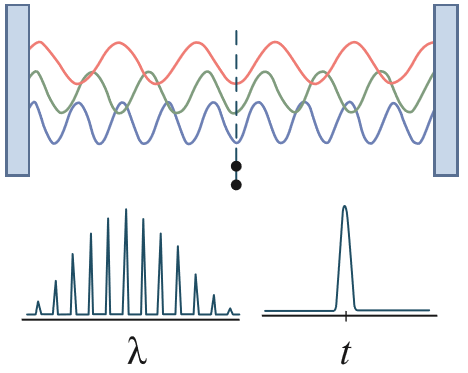
그림 2: 모드 동기(mode-locking)를 통해 극초단 펄스를 생산하는 기본 개념으로서 이러한 펄스는 시간적 폭은 극히 짧은데 반해 파장 대역폭이 매우 넓음
에너지가 E'0인 상태 χ0를 이에 상응하는 에너지 En을 가지고 있는 다른 상태 φn으로 시스템을 전환시키는 가우시안 극초단 레이저 펄스를 고려할 경우 파동함수는 다음과 같이 계산됩니다.
여기서 αn은 해당 펄스를 적용한 후 계수의 제곱이 개별 고유치(eigenstates)의 집단 확률을 나타내는 고유치 φn의 진폭을 가리킵니다. 1차 섭동론(first-order perturbation theory)에 따르면 이 고유치는 다음과 같이 구할 수 있습니다.
여기서 C는 펄스의 간섭장 진폭과 전이 쌍극자 모멘트에 의존하는 상수를 가리키며, α = 2π2 / ln(2)입니다. < φn | χ0 >는 초기 상태와 최종 상태 간의 적분으로 얻게 되는 프랑크-콘돈 인자(Franck-Condon factor)입니다. 방정식 2에 있는 적분을 계산하면 다음과 같습니다.
여기서 ωn = (En - E'0) / ℏ는 보어 진동수(Bohr frequency)를 가리킵니다. 극초단 펄스의 범위 내에서 레이저가 여기될 경우 프로세스의 수명은 0에 근접하며, αn = C < φn | χ0 >입니다. 따라서 초기 파동함수와 동일한 형태를 갖게되는 여기 파동 패킷 ψ는 여기된 고유 상태가 결맞음 중첩(coherent superposition)이 된 것을 의미합니다.
위 공식을 바탕으로 한 극초단 펄스의 간섭성은 다단계 원자5, 분자6, 반도체 스핀 상태7, 위상 전이8, 자성9을 제어할 수 있는 강력한 기법을 제공하며, 이전의 기술로는 불가능했던 어플리케이션을 구현할 수 있도록 합니다. 극초단 레이저를 활용하면 신소재의 구조적 기능에 대한 패러다임을 좀 더 자세히 파악할 수 있어 원자, 분자, 단분자층의 역학적 조작을 통한 최적의 기능성 소재 설계가 가능해집니다.10,11 이처럼 원자 및 전자의 역학을 정확하게 연구 및 제어할 수 있는 능력이 초정밀 계측 기법과 고기능성 소재 기반의 다양한 첨단 신기술을 이끌어온 것이나 다름없습니다.
참고문헌:
- B. Pullman, (1998). The Atom in the History of Human Thought. Oxford, England: Oxford University Press.
- H. C. von Baeyer, Taming the Atom; Random House: New York, 1992.
- A. H. Zewail, J. M. Thomas, 4D Electron Microscopy. Imaging in Space and Time; Imperial College Press, 2010.
- T. E. Karam, Ultrafast and Nonlinear Spectroscopy of Colloidal Nanomaterials. (2016).
- M.C. Stowe, A. Pe’er, J. Ye, Phys. Rev. Lett. 100, 203001 (2008).
- M. Viteau, A. Chotia, M. Allegrini, N. Bouloufa, O. Dulieu, D. Comparat, P. Pillet, Sci. Agric. 321, 232 (2008).
- D. Press, K.D. Greve, P.L. McMahon, T.D. Ladd, B. Friess, C. Schneider, M. Kamp, S. Höfling, A. Forchel, Y. Yamamoto, Nat. Photonics. 4, 367 (2010).
- J. Hu, G. M. Vanacore, Z. Yang, X. Miao, A. H. Zewail. ACS Nano 9, 6728 (2015).
- Kimel, A. V., A. Kirilyuk, P. A. Usachev, R. V. Pisarev, A. M. Balbashov, Th. Rasing. Nature 435, 7042 (2005).
- Hu, J., Karam, T.E., Blake, G.A. and Zewail, A.H., Chem. Phys. Lett. 683, 258 (2017).
- Kaplan, M., Yoo, B.K., Tang, J., Karam, T.E., Liao, B., Majumdar, D., Baltimore, D., Jensen, G.J. and Zewail, A.H. Angew. Chem. Int. Ed. 56, 11498 (2017).



























본사 및 지사별 연락처 확인하기
견적 요청 도구
재고 번호 입력 필요
Copyright 2023, 에드몬드옵틱스코리아 사업자 등록번호: 110-81-74657 | 대표이사: 앙텍하우 | 통신판매업 신고번호: 제 2022-서울마포-0965호, 서울특별시 마포구 월드컵북로 21, 7층 (서교동, 풍성빌딩)