색 수차와 단색 광학 수차

광학 시스템을 설계하는 작업은 결코 만만한 일이 아닙니다. 즉 완벽한 디자인의 시스템이라도 광학 수차는 존재하기 마련입니다. 최적의 시스템을 생성하기 위한 최고의 방법은 광학 수차를 제대로 이해하고 보정하는 것입니다. 이를 위해서는 우선 광학 시스템에 존재하는 광학 수차의 유형을 검토해야 합니다.

광학 수차는 완벽한 수학적 모델과의 편차를 의미합니다. 이러한 편차는 물리적, 광학적 혹은 수학적 결함이 원인이 아니라는 점을 유의해야 합니다. 오히려 렌즈 자체의 형태, 빛의 파동 특성 또는 시스템 내에서의 광학 요소 배치로 인해 발생할 가능성이 있습니다. 광학 시스템은 이미지의 크기와 위치를 구하기 위해 일반적으로 1차 혹은 근축 광학을 이용하여 설계됩니다. 근축 광학의 경우에는 광학 수차를 고려하지 않습니다. 이는 광선을 빛으로 취급함에 따라 수차를 유발하는 파동 현상은 제외시키기 때문입니다.

광학 수차의 이름과 특성은 다양한 방식으로 지정됩니다. 수차를 단순하게 두 그룹으로 분류하자면, 색 수차(두 개 이상의 파장광을 사용할 때 나타남)와 단색 수차(단일 파장광을 사용할 때 나타남)로 나뉠 수 있습니다.

색 수차

색 수차(Chromatic aberration)는 더 나아가 횡방향과 종방향의 두 가지 유형으로 분류됩니다. 종방향은 1차 혹은 2차 종방향 색수차로 다시 구분될 수 있습니다.

횡방향 색수차(TCA: Transverse Chromatic Aberration)는 이미지의 크기가 파장에 따라 변화할 때 발생합니다. 다시 말해 백색광을 사용하면 적색, 황색 및 청색 파장은 수직면에서 개별 지점에 초점을 맞춥니다(그림 1). 광학 용어에서 656.3nm (적색)는 C 라이트, 587.6nm (황색)는 d 라이트, 그리고 486.1nm (청색)는 F 라이트로 간주합니다. 이러한 명칭은 C & F 라이트에 대한 수소 방출 라인과 d 라이트에 대한 헬륨에서 비롯됩니다.

종방향 색수차(LCA: Longitudinal Chromatic Aberration)는 유리의 분산 특성의 결과로 서로 다른 파장이 수평 광학 축을 따라 다른 지점에서 초점을 맺을 때 발생합니다. 유리의 굴절률은 파장에 따라 다르기 때문에 파장광이 초점을 맞추는 위치에 따라 미치는 영향력이 약간씩 차이가 있음으로써 수평면을 따라 F, d 및 C 라이트는 별도의 초점(focal point)을 갖게 됩니다(그림 2).

Transverse Chromatic Aberration of a Single Positive Lens

그림 1: Single Positive Lens의 횡방향 색수차

Longitudinal Chromatic Aberration of a Single Positive Lens

그림 2: Single Positive Lens의 종방향 색수차

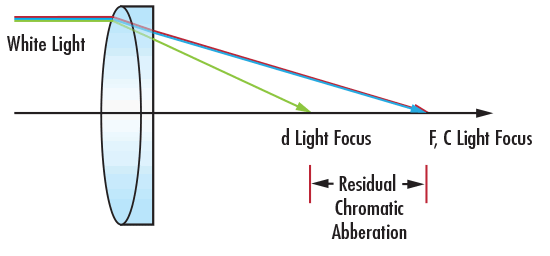
Achromatic Doublet Lens Correcting for Primary Longitudinal Chromatic Aberration

그림 3: Achromatic Doublet Lens로 1차 종방향 색수차 보정

1차 종방향 색수차의 보정은 일반적으로 굴절률이 다른 positive lens와 negative lens 요소로 구성된 achromatic doublet lens를 사용해 수행됩니다(그림 3). 이러한 유형의 보정은 동일한 위치에 F와 C 라이트의 초점이 맺히도록 하지만 잔류 색수차를 유발하는 d 라이트 초점의 위치에는 거의 영향을 미치지 않습니다.

잔류하는 종방향 색수차를 보정하기 위해서는 더욱 복잡한 렌즈나 렌즈 시스템을 이용해야만 빛의 초점을 이동시켜가며 F와 C 포커스와 동일한 축에 위치시킬 수 있습니다. 이와 같은 보정을 위해서는 동일한 지점에서 3개 파장의 초점을 맞추는 apochromatic lens를 사용하거나 동일한 지점에서 4개 파장의 초점을 맞추는 superachromatic lens를 사용해 수행할 수 있습니다. 그림 4a - 4d에서는 앞서 다룬 렌즈 시스템 유형들 간의 초점 이동을 비교해서 보여줍니다.

Focus Shift Illustration of No Aberration Correction with a Singlet Lens

그림 4a: Singlet Lens로 수차 보정 없이 초점을 이동시킨 모습

Focus Shift Illustration of Primary Longitudinal Chromatic Aberration Correction with an Achromatic Lens

그림 4b: Achromatic Lens로 1차 종방향 색수차 보정을 위해 초점을 이동시킨 모습

Focus Shift Illustration of Secondary Longitudinal Chromatic Aberration Correction with an Apochromatic Lens

그림 4c: Apochromatic Lens로 2차 종방향 색수차 보정을 위해 초점을 이동시킨 모습

Focus Shift Illustration of Secondary Longitudinal Chromatic Aberration Correction with a Superachromatic Lens

그림 4d: Superachromatic Lens로 2차 종방향 색수차 보정을 위해 초점을 이동시킨 모습

단색 수차

단색 수차(Monochromatic aberration)는 색 수차에 비해 훨씬 더 많은 유형으로 존재합니다. 이에 따라 단색 수차에는 명칭 뿐만 아니라 웨이브프런트 계수도 함께 표시됩니다. 예를 들어 구면 수차의 웨이브프런트 계수는 $ \small{W_{040}} $입니다. 이러한 웨이브프런트 계수는 완벽한 웨이브프런트와 수차가 있는 웨이브프런트 사이의 실제 차이를 알려주는 수학적 합계로 구해집니다:

(1)$$ W = \sum_{l + k +m = 0} ^{\infty} { \bigg[ W_{klm}\cdot H^k \cdot \rho^l \cdot \cos ^m \left( \theta \right) \bigg]} $$

공식 1에서 $ \small{W_{klm}} $은 웨이브프런트 계수, $ \small{H} $는 정상화된 이미지의 높이, $ \small{\rho} $는 동공의 위치, 그리고 $ \small{\theta} $는 두 벡터의 외적에 따라 도달할 경우 두 벡터 사이의 각도를 의미합니다. 일단 웨이브프런트 계수를 알고 있다면 I와 $ \small{k} $를 추가해 차수(order number)를 구할 수 있습니다. 그러나 이러한 방식은 항상 짝수를 만들어 냅니다. 광학 차수는 대개 1차, 3차, 5차 등으로 칭해지기 때문이 $ \small{k + 1 = 2} $일 경우에는 1차 수차가 되고 $ \small{k+1=4} $일 경우에는 3차 수차가 됩니다. 일반적으로 시스템 분석에는 1차와 3차 수차만 필요합니다. 더 높은 차수의 수차가 존재하긴 하지만 시스템이 복잡해지기 때문에 고수차의 광학 시스템은 일반적으로 보정을 하지 않습니다. 고차수의 수차를 보정하는 복잡한 보정 작업이 이미지 품질 개선에 도움이 되지는 않기 때문입니다. 표 1에는 일반적인 3차 단색 수차와 이에 상응하는 계수 및 관련 공식이 나열되어 있습니다.

Aberration Name	Wavefront Coefficient	Equation
Tilt	$$ W_{111} $$	$$ W_{111} \cdot H \cdot \rho \cdot \cos{\left( \theta \right)} $$
Defocus	$$ W_{020} $$	$$ W_{020} \cdot \rho ^2 $$
Spherical	$$ W_{040} $$	$$ W_{040} \cdot \rho ^4 $$
Coma	$$ W_{131} $$	$$ W_{131} \cdot H \cdot \rho ^3 \cdot \cos{\left( \theta \right)} $$
Astigmatism	$$ W_{222} $$	$$ W_{222} \cdot H^2 \cdot \rho^2 \cdot \cos^2{\left( \theta \right)} $$
Field Curvature	$$ W_{220} $$	$$ W_{220} \cdot H^2 \cdot \rho^2 $$
Disortion	$$ W_{311} $$	$$ W_{311} \cdot H^3 \cdot \rho \cdot \cos{\left( \theta \right)} $$

표 1: 일반적인 3차 광학 수차

광학 시스템과 이미징 시스템에는 광학 수차가 여러 가지 조합으로 포함되어 있을 수 있습니다. 이러한 광학 수차는 색 수차나 단색 수차로 분류할 수 있습니다. 수차가 존재하면 이미지의 품질이 저하되고 광학 설계 작업 중 상당 부분이 광학 수차를 파악하고 줄이는 데 집중됩니다. 수차 보정을 위한 첫 번째 단계는 바로 수차의 유형을 알아내고 시스템에 영향을 미치는 방식에 대해 이해하는 것입니다. 이러한 지식을 가지고 있어야 최상에 가까운 시스템을 설계할 수 있습니다. 색 수차와 단색 수차의 식별과 보정에 관한 심도 있는 정보는 광학 수차의 비교에서 자세히 다룹니다.

참고 자료

Dereniak, Eustace L., and Teresa D. Dereniak. Geometrical and Trigonometric Optics. Cambridge: Cambridge University Press, 2008.

본 콘텐츠가 도움이 되었습니까?

본 콘텐츠를 평가해주셔서 감사합니다!