광학 수차의 비교
광학적 수차는 수학적으로 완벽한 모델에서 나타나는 편차입니다. 여기서 주의해야할 것은 이러한 편차가 물리적, 광학적 혹은 기계적 결함으로 인해 발생하는 것이 아니라는 점입니다. 오히려 렌즈의 형태 자체가 원인이 되거나 빛이 지닌 파동 특성 때문에 시스템 내에서 광학 요소를 배치하면서 발생할 수 있습니다. 광학 시스템을 설계할 때 이미지의 크기와 위치를 계산하기 위해서는 주로 첫 번째 차수 혹은 근축 광학이 사용됩니다. 근축 광학(paraxial optics)은 빛을 광선으로 취급하고 광학 수차의 발생을 고려하지 않으므로 수차를 일으키는 파동 현상은 제외시킵니다. 광학 수차에 대한 소개는 색 수차 및 무색 광학 수차 편에서 자세히 다룹니다.
색 수차와 무색 광학 수차를 여러 개의 그룹과 유형으로 나뉘어 정의한 뒤 컴퓨터 분석이나 실제 관찰을 통해 문제가 되는 부분을 발견 후 이를 시스템이 인식하면서 수차를 줄이기 위한 시스템의 보정이 이루어집니다. 일반적으로 광학 설계자는 우선 Zemax®나 Code V®와 같은 광학 시스템 디자인 소프트웨어에 시스템을 설치하여 시스템의 성능과 수차를 확인합니다. 광학 수차는 광학 부품이 제작된 후 시스템의 출력을 관찰하면서 감지된다는 점에 주의하십시오.
광학 수차의 감별
대개는 사용 중인 시스템에 두 가지 이상의 수차가 존재하기 때문에 광학 시스템에 존재하는 수차를 구별하는 작업이 절대 쉬운 일이 아니며 컴퓨터 분석 단계에서 조차도 식별에 어려움이 따릅니다. 이러한 수차를 파악하고 보정 작업을 하기 위해 광학 설계자는 computer generated spot diagram, wave fan diagram, ray fan diagram과 같은 다양한 종류의 도구를 활용합니다. Spot diagram은 시스템으로 이미징 처리된 후에 빛의 단일 지점이 어떻게 나타나는지를 보여줍니다. Wave fan diagram은 완벽한 파동이 x 방향을 따라 평평하게 되는 위치에서 일반 웨이브프런트를 평평한 웨이브프런트와 비교해서 보여줍니다. Ray fan diagram은 ray fan을 pupil 좌표와 비교하는 점들로 구성된 도표입니다. 아래의 이미지는 수차마다 가 1이 되는 tangential (수직, y 방향)과 sagittal (수평, z 방향) plane을 표현한 대표적인 wave fan과 ray fan diagram으로서 여기서 적용된 수차는 tilt , defocus , spherical , coma , astigmatism , field curvature , distortion 입니다. 간단히 관심있는 수차를 선택하면 해당 그래프를 확인할 수 있습니다.
수차 종류 (웨이브프런트 계수):

그림 1: Airy Disk의 패턴
특히 시스템의 설계 단계에서는 수차를 알아내는 것이 수차 보정을 위한 첫 번째 작업입니다. 광학 설계자가 수차 보정을 하고자하는 이유는 무엇일까요? 이는 가능한 최상의 성능을 발휘할 수 있도록 회절 제한 시스템을 생성하기 위해서입니다. 회절 제한 시스템은 모든 수차를 Airy disk 크기 또는 원형 구경에 의해 발생하는 회절 패턴 크기 이내로 억제합니다(그림 1).
방정식 1은 Airy disk spot size 를 구하는 데 사용되며, 여기서 λ는 시스템에서 사용되는 파장 그리고 f/#는 시스템의 f-넘버입니다.
광학 수차 예제
시스템을 설계하고 제작한 후에는 레이저와 같은 점광원(point source)을 이미징해 수차를 관찰하면서 이미지 면에 단일 점이 어떻게 나타나는지를 시스템을 통해 확인할 수 있습니다. 다양한 수차가 존재하더라도 일반적으로 이미지가 스팟 형태에 가까울수록 수차의 발생은 줄어들게 됩니다. 단, 시스템으로 스팟을 확대할 수 있기 때문에 스팟의 크기하고는 관련이 없습니다. 아래의 7가지 예제는 시스템 내에 존재하는 해당 수차가 단 한 가지인 경우에 일반 테스트 타깃(그림 2 - 4)을 이용해 수차가 존재하는 이미지의 시뮬레이션, 광선의 동작 그리고 수차를 최소화하는 보정 방법에 대해 설명해줍니다.
Code V®로 생성된 시뮬레이션은 유발된 수차를 보다 잘 보여주기 위해 이를 과장해서 표현합니다. 단, 고차원의 수차를 보정하는 과정은 더욱더 복잡하고 이미지 품질의 향상이 미미하기 때문에 본문에서는 보편적으로 알고 있는 1차와 3차 수차에 관해서만 다룹니다.

그림 2: Fixed Frequency Grid Distortion Target

그림 3: Negative Contrast 1951 USAF Resolution Target

그림 4: Star Target
| Tilt – | |
 그림 5a: Tilt 수차의 표현 |
 그림 5b: Tilt 수차의 시뮬레이션 |
특성
|
보정 방법
|
| Defocus – | |
 그림 6a: Defocus 수차의 표현 |
 그림 6b: Defocus 수차의 시뮬레이션 |
특성
|
보정 방법
|
| Spherical – | |
 그림 7a: 구면 수차의 표현 |
 그림 7b: 구면 수차의 시뮬레이션 |
특성
|
보정 방법
|
| Coma – | |
 그림 8a: Coma 수차의 표현 |
 그림 8b: Coma 수차의 시뮬레이션 |
특성
|
보정 방법
|
| Astigmatism – | |
 그림 9a: Astigmatism 수차의 표현 |
 그림 9b: Astigmatism의 시뮬레이션 |
특성
|
보정 방법
|
| Field Curvature – | |
 그림 10a: Field Curvature 수차의 표현 |
 그림 10b: Field Curvature 수차의 시뮬레이션 |
특성
|
보정 방법
|
| Distortion – | |
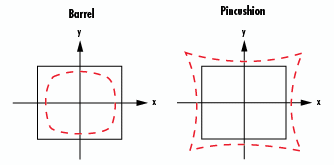 그림 11a: Distortion 수차의 표현 |

그림 11b: Barrel Distortion 수차의 시뮬레이션 
그림 11c: Pincushion Distortion 수차의 시뮬레이션 |
특성
|
보정 방법
|
회절 제한 성능을 갖춘 시스템을 구현하기 위해서는 광학 수차를 발견하고 이를 보정하는 작업이 무엇보다 중요합니다. 광학 및 이미징 시스템에는 색 수차 혹은 무색 수차로 구분되는 다양한 조합의 광학 수차가 존재할 수 있습니다. 광학 수차 보정 작업은 aperture stop을 이동시키고 광학 렌즈의 유형을 변경하는 단계에서 광학 수차의 수와 수준(강도)을 대폭 줄일 수 있기 때문에 설계 단계에서 가장 수월하게 진행됩니다. 차수가 높은 수차를 감소시키면 과정이 더 복잡해지고 이미지 품질의 향상이 미미하기 때문에 전반적으로 광학 설계자는 우선 1차와 3차 수차를 줄이는 데 주력해야합니다.
참고 문헌
- Dereniak, Eustace L., and Teresa D. Dereniak. Geometrical and Trigonometric Optics. Cambridge: Cambridge University Press, 2008.




































































































1-800-363-1992
본사 및 지사별 연락처 확인하기
견적 요청 도구
재고 번호 입력 필요
Copyright 2025, 에드몬드옵틱스코리아 사업자 등록번호: 110-81-74657 | 대표이사: 앙텍하우 | 통신판매업 신고번호: 제 2022-서울마포-0965호, 서울특별시 마포구 월드컵북로 21, 7층 (서교동, 풍성빌딩)