Laser Polarization: The Importance of Polarization in Laser Applications
저자: Hayden Kim
Light can be understood as a transverse electromagnetic wave composed of oscillating electric and magnetic fields. The orientation of the electric field in the light wave is described by the light's polarization. Many light sources including sunlight, halogen lighting, and LED spotlights are considered unpolarized because the orientation of their electric fields fluctuates randomly in time. Laser sources, on the other hand, are often linearly polarized.
Understanding laser polarization is important for many applications, as polarization impacts reflectance, the focus of laser beams, and other optical behaviors that affect end applications of the laser. While most laser sources are linearly polarized, other classifications of polarization can also be generated, such as circular, elliptical, and radial polarization. The basic principles of polarization are covered in our Introduction to Polarization application note, but this guide dives into the specific application of those concepts to laser applications.
Polarization of Laser Sources
The state of a laser's polarization is determined by several anisotropic mechanisms of either the laser gain media or the resonator. "Anisotropic" refers to properties whose values vary in different directions. A laser gain medium may be polarization-dependent, as is the case with some anisotropic laser crystals and semiconductor optical amplifiers. Inside this medium, emission is stimulated by incoming pump photons. Stimulated emission photons will be emitted in the same polarization state as that of the pump photons. With the absence of polarization-selection optics, such as polarizers and waveplates (also called retarders), light would be unpolarized and unsuitable for certain applications. In addition, losses in the resonator, from the inclusion of a Brewster plate or a slight misalignment of any other optical components involved, can be responsible for changes in polarized laser emissions.
The polarization extinction ratio can be used to determine the degree of polarization after propagation through a device or system, such as a laser cavity. It is the ratio of the optical power in the principal polarization mode to the orthogonal polarization mode, where each of these modes are perpendicular to each other. These polarizations are usually called TE (transverse electric) and TM (transverse magnetic). is often presented as a ratio of the two orthogonal polarization states (such as 100:1, indicating the amount of light polarized in the principal direction is 100X that of the light in the orthogonal direction). For example, the of Coherent® High Performance OBIS™ LX/LS Laser Systems is 100:1, while the of the linearly-polarized Lumentum High Performance Helium-Neon Lasers is 500:1. can also be expressed in decibels, which is calculated using:
Polarization-Dependence of Reflectance
A single light wave consists of two independent, orthogonal components constituting the p- and s-polarization states, which are crucial in applications utilizing the reflection and transmission of certain polarizations of light. For p-polarized light, the electric field is parallel to the plane of incidence of an interface while the electric field is perpendicular to the plane for s-polarized light (Figure 1).

Figure 1: Depiction of s- and p-polarization, which are linear polarizations defined by their relative orientation to the plane of incidence. This figure also shows Brewster's angle, at which no p-polarized light is reflected at an optical interface.1
This is important to understand when dealing with light propagation at an interface between two media with the introduction of the Brewster’s angle. Brewster’s angle is an angle of incidence at which p-polarized light is transmitted through while s-polarized light is partially reflected at an uncoated optical surface (Figure 2). The concept is applied in laser cavities to fully transmit the p-polarized component of light and to introduce losses for the s-polarized component through reflection. Brewster’s angle can be determined by the indices of refraction of the incident medium through which the light propagates and another medium .

Figure 2: Fresnel reflectivity at an air-glass optical interface vs. angle of incidence. For p-polarization, the reflectivity vanishes at the Brewster angle (in this case, ~56°) while reflectivity for s-polarization steadily increases with increasing incidence angle.8
There are many optical components that utilize the concept of Brewster’s angle for useful applications. A Brewster window is a transparent substrate oriented at Brewster’s angle used when a beam of light propagates through a transparent window with minimal optical losses. For example, consider a Helium-Neon (He-Ne) laser with a sealed glass tube and external plano-convex mirrors. At the ends of the glass tube are transparent windows requiring less than 1% losses per pass. When Brewster windows are placed carefully on each side of the tube, reflectivity at the air-glass interfaces becomes nominal for p-polarized light, proving it beneficial to preventing interference effects from residual reflection within the resonator (Figure 3). The considerable loss differences between p- and s-polarizations induce the laser output to become p-polarized.
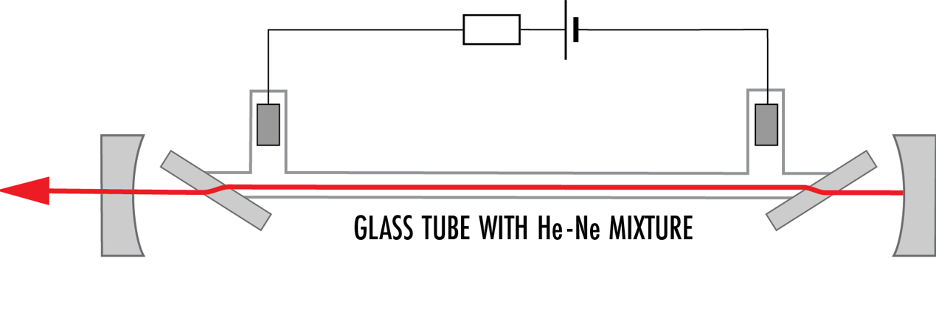
Figure 3: The laser system of a He-Ne laser with two Brewster windows having the same orientation within the laser resonator. P-polarized light is significantly transmitted, inducing an overall p-polarization orientation of the laser emission.
Similar to the Brewster window is the Brewster plate, which is usually inserted into a polarized laser beam so that the transmitted light will emerge p-polarized. However, unlike a Brewster window, the plate is comprised of coplanar surfaces. The plate introduces a parallel shift of the beam position proportional to the thickness of the plate (Figure 4). FrequentlyFrequently applied in laser resonators consisting of laser crystals with large cross-sectional area, Brewster plates introduce polarization losses for the s-component and force the laser beam to attain a stable linear polarization.

Figure 4: As a laser beam passes through a Brewster plate with an angle of incidence close to Brewster’s angle, the transmitted beam is p-polarized while the reflected beam is s-polarized due to reflection losses.
On the other hand, zero-phase shift mirrors reflect both p- and s-polarization equally. This maintains the polarization of the incident laser beam.
Polarization-Dependence f Laser Focusing
The polarization of a laser beam impacts how it is focused. Research from Qinggele et al. from 2015 showed that focusing circularly-polarized beams resulted in symmetric spots at the diffraction limit while linearly-polarized beams focused into elongated spots stretched out in the direction of polarization.9 These effects are slight and negligible in many applications, but precise applications require them to be considered so as to strive to obtain diffraction-limited focused spots.
Applications of Polarization in Laser Applications
Polarized laser output can be put to use in many useful applications in the laser optics industry.
Polarization Beam Combining
Also known as polarization coupling, the technique superimposes multiple linearly polarized laser beams and can be broken down into two subcategories: coherent and incoherent polarization combining.
In the case of coherent polarization combining, the orthogonal polarization states of two coherent beams are superimposed, resulting in a purely linear laser emission (Figure 5). This is only possible if the two injected beams are orthogonally linear-polarized with a phase difference of , where is an integer. Due to this output, the technique can be repeated multiple times to increase the overall power of the laser emission, which is also known as power scaling. This technique is used in power amplifier laser systems.
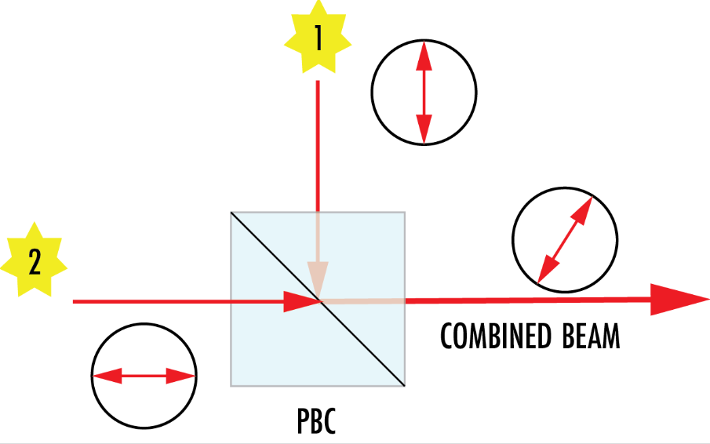
Figure 5: Two coherent laser beams are combined to produce a new linearly polarized output beam as they propagate through the polarization beam combiner (PBC).5
Incoherent polarization combining involves sending beams of different polarizations through a polarization beam combiner (PBC) to acquire an unpolarized beam displaying the combined optical power of the incident beams and a nearly doubled brightness. This technique involves polarized input beams and unpolarized emission and is therefore inapplicable for repeatable power scaling. For example, one vertically polarized beam and a horizontally polarized beam can be sent through a thin-film polarizer, resulting in one of the beams being reflected while the other is transmitted, with both beams propagating in the same direction.
Incoherent beam combination can be applied to end pumping a solid-state laser, where the pump light is injected along the direction of the beam rather than a transverse direction. Laser crystals made of materials such as Nd:YAG that can absorb pump radiation in both polarization directions can utilize this technique. For example, diode laser stacks, made up of multiple diode bars arranged in a 2D array of emitters to produce multi-kilowatt output power, suffer from lower overall brightness than that of an individual diode bar. Incoherent polarization beam combining can be applied to the stacks to improve the brightness, which in turn pumps high-power, solid-state bulk lasers.
Birefringence
Birefringence describes the optical property occurring in some transparent media where the index of refraction depends on the polarization of light, resulting in double refraction of light in the material. This phenomenon can be caused by a number of factors, including the crystal structure of the medium, stress fields intrinsic to– or induced in– the material, and the application of additional electromagnetic fields.
This property is utilized in devices called birefringent tuners, which narrow the optical bandwidth for transmission and reflect light of other wavelengths of a propagating intracavity laser beam. The tuner is placed at Brewster’s angle and then rotated about the axis perpendicular to the surface interface to induce a retardation at the narrowed transmitted wavelength. The wavelength of interest exhibits only the p-polarization component, leading to minimal or no reflection loss. In contrast, other wavelengths are subjected to a different retardation, become s-polarized, and undergo reflection losses. The tilt angle of the tuner influences the shift in wavelength for minimum loss in power and is adjusted on a mount equipped with a micrometer screw for precise modifications.
A single-plate tuner with an angle of incidence at Brewster’s angle is able to produce wavelength-dependent polarization changes through transmission losses for the s-polarization component of the laser beam. The thicker the tuner, the smaller the free spectral range which defines the spectral interval between two transmission maxima and offers better spectral resolution. The propagating laser beam undergoes slightly different propagations within the filter from its ordinary and extraordinary rays in which the former passes through unchanged while the latter is refracted at an angle. This leads to double refraction and uneven overlapping contributions to the output beam. Rotating the tuner around an axis perpendicular to the surface shifts the transmission curves and inevitably changes the direction of the extraordinary component of light.
Birefringent tuners can also be composed of multiple plates. The additional number of plates allow for the laser to operate at the target loss minimum. This is because, by increasing the thickness of the plates, the free spectral range decreases and the transmission minima on the range of wavelengths shifts closer. To further increase the reflection losses for unwanted wavelengths, polarizers can be inserted in between the plates. This configuration with certain constrained plate thicknesses become something called Lyot Depolarizers, which depolarize incident polychromatic polarized light.
Frequency Doubling
The concept of nonlinear polarization comes into play in the realm of frequency-doubled fiber lasers. Employed in certain lasers that utilize Nd:YAG and other nonlinear crystals as the lasing medium, frequency doubling produces a wave with twice the optical frequency as the pump light.
Lasers and Laser Polarization Optics at Edmund Optics®
Edmund Optics supplies a wide range of polarization optics including a variety of polarizers, waveplates, Brewster windows, and optical isolators ideal for laser applications.

Laser Sources
- Produce Coherent Light that Can Be Polarized or Unpolarized
- Many Laser Applications Depend on the Polarization State of the Output Beam
- Machine Vision Lasers, Life Science Lasers, Metrology Lasers, Gas Lasers, Industrial and Pointing Lasers, Material Processing Lasers, etc.
BUY NOW

 Brewster Windows
Brewster Windows
- Reduce Loss of P-Polarized Light
- Circular Profile When Oriented at 55.57°
- Great for Use in Laser Cavities
BUY NOW

Low Loss IBS Coated Thin Film Laser Polarizers
- 1064nm Nd:YAG Design Wavelength
- High Extinction Ratio of 10,000:1 @ 45° AOI
- Low Loss Ion Beam Sputtered (IBS) Coating
- UV Fused Silica Substrates with 10-5 Surface Quality
BUY NOW

Infrared (IR) Wire Grid Polarizers
- Designed for Wavelengths Ranging from 2 - 30μm
- Various Substrates Available
- 360° Rotation Using Metric Polarizer Mounts
BUY NOW

Rochon Polarizers
- Multiple Polarization Materials Available
- Ordinary Rays Pass Through Undeviated
- Extraordinary Rays Deviate
BUY NOW

Wollaston Polarizers
- Multiple Polarization Materials Available
- UV to IR Ranges Offered
- Large Deviation of Ordinary and Extraordinary Rays
BUY NOW

Achromatic Waveplates (Retarders)
- Multiple Wavelength Ranges Available
- Flat Response Over Each Broad Spectral Range
- λ/4 and λ/2 Retardance
- Mounted in Black Anodized Aluminum Housing
BUY NOW

Precision Zero Order Waveplates (Retarders)
- λ/4 and λ/2 Retardance
- Excellent Angular Field of View
- Birefringent Polymer Stack
- High Damage Threshold of 500 W/cm2
BUY NOW

Quartz Waveplates (Retarders)
- Zero Order and Multiple Order Waveplates
- λ/4 and λ/2 Retardance
- Mounted in Black Anodized Aluminum Frame
- Zero Order Polymer Waveplates Also Available
BUY NOW

Free-Space Optical Isolators
- Up to 67 dB Isolation for Ultimate Stability
- Up to 92% Transmission for Maximum Power
- 4.7mm Input Aperture
BUY NOW
Still not sure which products you need for your application? Contact us and an expert will answer your questions.
References
- Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
- Paschotta, Rüdiger: Field Guide to Lasers. SPIE Press, 2008.
- Collet, Edward: Field Guide to Polarization. SPIE Press, 2005.
- R. Uberna, A. Bratcher and B. G. Tiemann, "Coherent Polarization Beam Combination," in IEEE Journal of Quantum Electronics, vol. 46, no. 8, pp. 1191-1196, Aug. 2010, doi: 10.1109/JQE.2010.2044976.
- Pengfei Ma, Pu Zhou, Yanxing Ma, Rongtao Su, Zejin Liu, “Coherent polarization beam combining of four fiber amplifiers in 100ns pulsed-regime,” in Optics & Laser Technology, vol. 47, pp. 336-340, 2013, ISSN 0030-3992, https://doi.org/10.1016/j.optlastec.2012.08.030.
- Cieślak, Rafał & Clarkson, W.A.. (2011). “Internal resonantly enhanced frequency doubling of continuous-wave fiber lasers.” Optics letters. 36. 1896-8. 10.1364/OL.36.001896.
- A.G. Sedukhin, A.G. Poleshchuk, “Efficient tight focusing of laser beams optimally matched to their thin-film linear-to-radial polarization conversion: Method, implementation, and field near focus”, Optics Communications, Volume 407, pp. 217-226, 2018, ISSN 0030-4018, https://doi.org/10.1016/j.optcom.2017.09.042.
- S. Joseph, V. Michael, “Blue sun reflected from water: optical lessons from observations of nature” 2017, 250. 10.1117/12.2270481.
- Li, Qinggele, Ledoux-Rak, Isabelle, & Diep Lai, Ngoc, " Influence of incident beam polarization on intensity and polarization distributions of tight focusing spot", Advanced Device Materials, Volume1, pp. 4 – 10, 2015, DOI: 10.1179/2055031614Y.0000000002
Additional Resources
- Introduction to Polarization
- Polarizer Selection Guide
- Confocal Microscopy
- Differential Interference Contrast Microscopy
- Understanding Waveplates and Retarders
- Key Parameters of a Laser System
- Common Laser Types
- How to Build an Optical Isolator with Stock Components
- Introduction to the Laser Optics Lab Video Series




































































































































































































































본사 및 지사별 연락처 확인하기
견적 요청 도구
재고 번호 입력 필요
Copyright 2023, 에드몬드옵틱스코리아 사업자 등록번호: 110-81-74657 | 대표이사: 앙텍하우 | 통신판매업 신고번호: 제 2022-서울마포-0965호, 서울특별시 마포구 월드컵북로 21, 7층 (서교동, 풍성빌딩)